Skim some deeper math details

What have been refered to as "Tuples" like , can be viewed as binary quadratic forms, which are functions of two variables like so:

It turns out that when multiplying two of these objects, under some circumstances it is possible to obtain a third:

with x, y written as a bilinear combination of r,s,t,u.

This is a rich and interesting subject, but it turns out the cube equations capture this. Indeed, given a cube of integers, the corresponding and give three binary quadratic forms with the above relationship and the bilinear coefficients are the integer values on the cube corners.

To emphasize this, the concepts of composition and equivalence can be defined and explored solely from the viewpoint of solutions to the cube equations.

But first, a closer look at how the forms relate to the cube values:

The cube of integers can be sliced three different ways into a pair of faces. And the three choices here give the three different forms.

This was first noted by Bhargava, and these objects are often called Bhargava cubes.

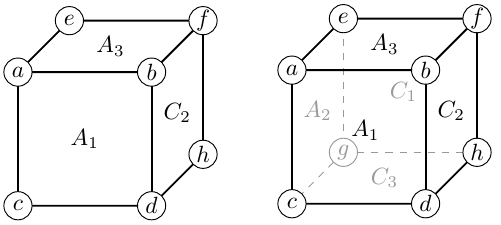
where the orientation of the matrices is chosen to fix a,h in the upper-left and lower-right respectively.

From this, the transformations seen previously should be clearer now. Since , multiplying both faces of a form by a matrix with determinant 1 will not change the value of the determinant; it will not change the form.

Looking at composition in terms of forms:

there is an additional freedom not discussed above. x,y (in terms of r,s,t,u) can be swapped if (A3,B3,C3) is reversed. It turns out one choice is more natural, as it leads to the composition on the equivalence class of the forms, being a mathematical group.

The cube equations, due to the symmetry, treat all three forms the same. While the "form composition" equation, breaks this symmetry with "two in, one out". What is going on here is that the cube relation is more naturally stated as the composition of all three forms is the "identity" form in this group.

where I(x,y) is the identity form. The cube therefore fixes the natural order of (A3,B3,C3).

It turns out that in the group, that (C3,B3,A3) is the inverse of (A3,B3,C3); that is they compose to the identity form. Therefore we can go from form1 form2 form3 = Id to form1 form2 = inverse_form3.

So to break the symmetry of the cube equations, to put it in terms of "two in, one out", we just need to reverse the order of one of the form’s coefficients.

Now returning to looking solutions to the cube equations, and trying to extract the main concepts purely from properties of those equations.

It can be proven that if given (A2,B2,C2) and (A3,B3,C3) such that

then necessarily

This can be use to define the following property: define (C1,B1,A1) to be the "composition" of the tuples (A2,B2,C2), (A3,B3,C3) if such a cube exists.

Due to symmetry of the cube and the equations, this can also be said for the other tuples. Given a solution, we can also say (C2,B2,A2) is a "composition" of the tuples (A1,B1,C1), (A3,B3,C3). And (C3,B3,A3) is a "composition" of the tuples (A1,B1,C1), (A2,B2,C2).

By expanding the tuple values in terms of the cube values, it can be checked that for any solution:

This value is called the discriminant. As mentioned above, this value is important for the existence of solutions given just two tuples. So in what follows, let’s restrict consideration of tuples to those of some given discriminant. For convenience, and to match additional assumptions that are given for the inputs to our math puzzle, the discriminant will be taken to be -p where p is a prime number.

With this restriction going forward, for any two tuples under consideration there will always exist a third which is a composition of those two tuples.

Define two tuples (A,B,C) and (A',B',C') to be "equivalent" if there exists two other tuples T1 and T2 such that (A,B,C) is a composition of T1 and T2, and (A',B',C') is also a composition of T1 and T2. We will denote that two tuples are equivalent by writing tuple1 ~ tuple2.

The composition property respects the equivalence relation in the following way. If T1 ~ T2 and T3 ~ T4, then any tuple which is a composition of T1 and T3 is equivalent to any tuple which is a composition of T2 and T4.

We can rewrite this more cleanly if we define "*" between tuples to mean composition, so that (tuple1 * tuple2) as an operation results in some tuple such that it is the composition of tuple1 and tuple2. The previous result can then be written:

It turns out that this operation has nice properties.

Reminding that we are restricting to considering the set of tuples with a particular discriminant, we can further say

Now consider two cubes given by the tuples T1a,T1b,T1c and T2a,T2b,T2c respectively. Then we have:

and so composition of tuples, along with existence of a cube for any three tuples that satisfy a composition relation, means that given two cubes a third exists which is a "composition" of two other cubes.

This bears repeating: the cube equations not only lead us to composition of forms, but it shows these must exist a composition of entire cubes.

It is this cube composition which the algorithm contest involves.

In the competition, your function will be given (a,b,c,d,e,f,g,h) specifying a cube, with the guarantee that the first two tuples are equal (A1,B1,C1) = (A2,B2,C2).

Using cube composition, a new cube must be calculated such that

Note: